EXECUTIVE SUMMARY

• A review of possible rules and estimated economic impacts shows that the Trump Administration’s fiscal year 2020 regulatory budget accounting will rely on just a handful of rules.
• Savings will primarily come from finalization of the Safer Affordable Fuel-Efficient Vehicles Rule, which it appears will save about $80 billion.
• On the cost side of the ledger, the Department of Homeland Security will impose $35.2 billion mostly from rules aimed at restricting immigration.

INTRODUCTION

The Trump Administration recently unveiled its fiscal year (FY) 2020 regulatory budget. Its cumulative savings target, at $51.6 billion in net present value savings, would more than double the savings of all previous Trump Administration regulatory budgets combined. But a closer look at the individual agency targets that make up that large sum shows just a few agencies largely drive the final results.

This study uses the regulatory budget, the Fall 2019 Unified Agenda of Regulatory and Deregulatory Actions (which lists the rules likely to be finalized over the next year), and the American Action Forum’s Regulation Rodeo database to determine which individual rules are likely to have the most effect on the final accounting.

FY 2020 BUDGET OVERVIEW

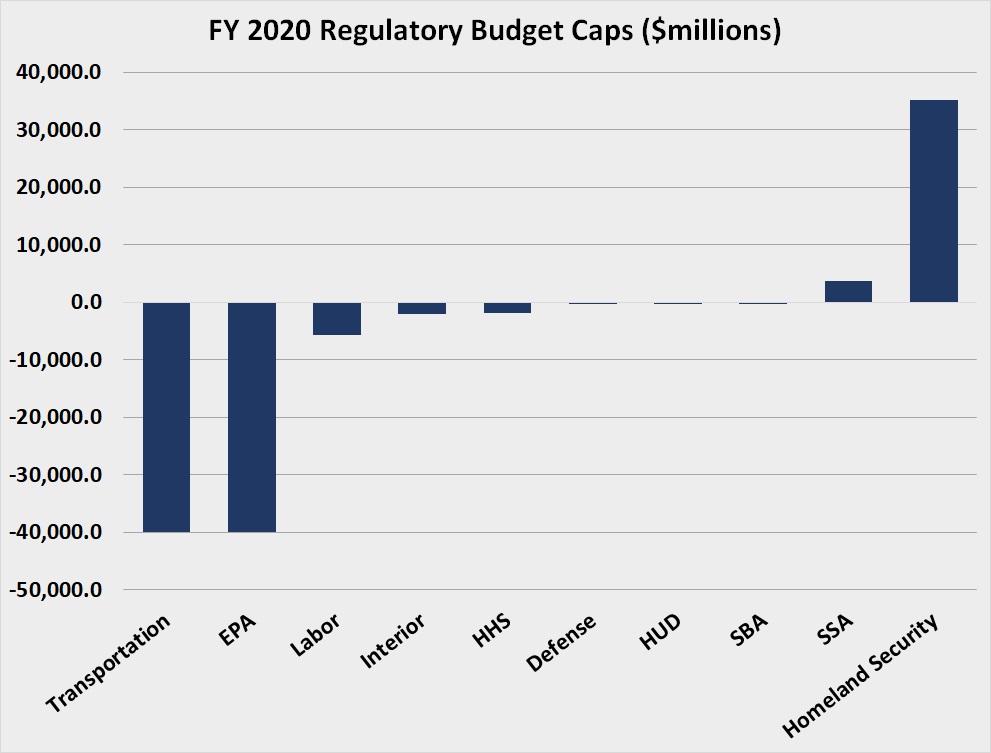
The regulatory budget is a cap on the amount of costs the administration’s regulations can impose on the economy. The Trump Administration has established a negative cap, or a savings target, of $51.6 billion for FY 2020. This total is calculated by summing the targets of each agency in the budget. For FY 2020, 10 agencies have a target other than $0. These agencies, and their targets, are shown in the chart below:

What immediately stands out in this chart are the outliers at each end. The Department of Transportation (DOT) and the Environmental Protection Agency (EPA) each have savings targets of $40 billion, while the Department of Homeland Security (DHS) has a cost cap of $35.2 billion. These extremes are unprecedented in the three years of regulatory budgeting. It is worth examining these agencies to determine what rules will drive such large savings and costs.

UNPRECEDENTED SAVINGS FROM ONE RULE

Only one rule in the regulatory agenda is expected to be large enough to lead to the savings expected in FY 2020 from DOT and EPA. Those agencies are jointly working on the Safer Affordable Fuel-Efficient (SAFE) Vehicles rule, which when proposed was estimated to save about $370 billion in net present value (using the 7 percent discount rate preferred under regulatory budget accounting). It was so large that in its FY 2019 regulatory budget the administration planned to not include it in the final accounting so as to not skew the overall numbers. According to news reports, the agencies are expected to dial back the deregulatory effect of the rule when finalized. Based on the savings targets of DOT and EPA, it appears the rule will now save about $80 billion – split evenly between the two agencies for regulatory budgeting purposes. Though DOT and EPA are expected to finalize other rules that in a more typical fiscal year would likely affect the regulatory budget, the SAFE Vehicles rule renders them relatively minor in the scope of FY 2020.

The rule is still so large it more than covers the savings target by itself. Without it, executive agencies are projected to issue about a combined $28 billion in costs. As the chart above shows, we can look to DHS to figure out where those costs will come from.

RESTRICTED IMMIGRATION COMES AT A HEFTY PRICE

The substantial costs from DHS likely come from one agency – U.S. Citizenship and Immigration Services (USCIS). This agency is working on three particularly expensive rules. The costliest is a rule that would double the length of time an asylum seeker must wait before applying for work authorization. When proposed last month, its expected total cost was $45.1 billion.

The second rule from USCIS would increase fees on many of the forms and applications associated with the immigration process ($11.4 billion in estimated costs when proposed). A third rule would get rid of the agency’s 30-day limit to consider applications for employment authorization from asylum seekers, at a proposed cost of $4.4 billion.

Combined, the costs of these proposed rules are more than $60 billion. In order to get down to the $35 billion cap called for by the regulatory budget, DHS might not finalize one, or perhaps even both, of the second two rules in FY 2020. Otherwise, there must either be additional deregulatory actions with savings, downward revisions to the estimated costs of the three rules that will occur before finalization, or some combination of the two. Based on the estimated savings of the proposed versions of the other rules listed in DHS’s regulatory agenda, however, none rise to a level significant enough achieve the required savings. The largest is a Coast Guard rule that would provide more flexibility on who can be in charge of fuel oil transfers on inspected vessels, at a savings of $250.4 million.

OTHER NOTABLE RULES IN FY 2020

While DOT, EPA, and DHS will disproportionately affect the FY 2020 regulatory budget numbers, other agencies will issue rules with notable costs and savings.

On the savings side of the ledger, the Department of Labor has the most expected of the remaining agencies at $5.7 billion. Based on the estimated savings of proposed rules, the largest contributor will be a rule that allows pension plan managers to make electronic disclosures to participants ($2.4 billion). Two others provide companies with flexibility regarding how they calculate hours worked in fluctuating workweeks ($884.7 million) and determine employees’ regular rate of pay (recently finalized with savings of $250.5 million). These savings will be offset somewhat by a rule defining joint-employer status ($412.1 million in costs).

The Department of Health and Human Services (HHS), the agency with the largest savings in each of the last two fiscal years, is expected to be net deregulatory once again. It is likely to finalize an action regarding Nondiscrimination in Health and Health Education Programs and Activities ($3.6 billion in estimated savings when proposed). HHS will also finalize some expensive rules. One implementing the 21^st Century Cures Act had an estimated $3.7 billion price tag when proposed. Another requiring health plans to disclose the cost of services and procedures was estimated to cost $1.8 billion. HHS will need to finalize offsetting deregulatory actions to reach its savings target of $1.9 billion.

One oddity is the Social Security Administration (SSA). With a cost cap of $3.7 billion, it is the only agency other than DHS with projected net costs. But unlike the other agencies above, it is not clear what rule may be coming that would impose such costs. None of the 13 rules listed in the Unified Agenda are marked as regulatory. A review of SSA’s previously proposed rules does not reveal any candidates, either. For now, the budgeted costs remain a mystery.

CONCLUSION

The Trump Administration’s FY 2020 $51.6 billion savings target is eye-popping. A closer look shows that just a handful of rules will largely drive the final tally at the end of the fiscal year, if the proposed versions of those rules are any guide. As always, however, one should expect a few surprises that could notably alter the results.