Summary:

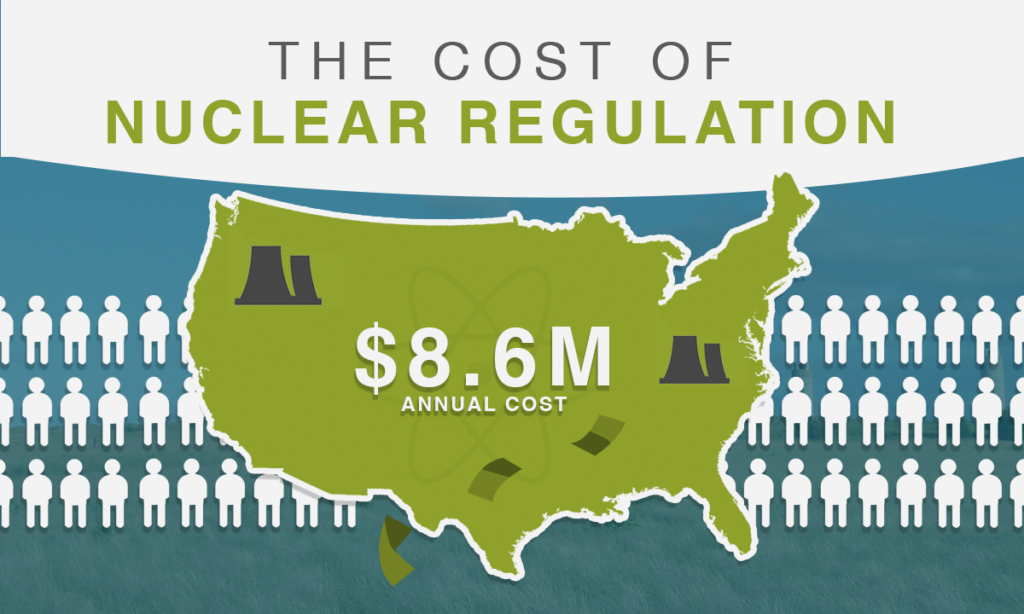
• The average nuclear power plant must comply with a regulatory burden of at least $8.6 million annually.
• Currently, construction of a new plant begins after waiting for nearly a decade for regulatory approval.
• While there are good reasons for nuclear security rules, nuclear energy is being placed at a distinct disadvantage compared to other fuel sources.
• Although the total listed costs from Nuclear Regulatory Commission (NRC) rules imposed on the industry since 2006 are just $444 million, regulations from other agencies, fees, security costs, and the industry’s unfavorable treatment under the Clean Power Plan make competition in today’s energy market a struggle.

The Costs

Nuclear Regulation at a Glance (costs per plant)
Paperwork Costs	$4.2 million
Security Costs (wages only)	$4.4 million
Fees	$22 million

As with many independent agencies, there is much the public doesn’t know about the costs and benefits of new rules. As mentioned, Regulatory costs imposed on nuclear power plants by the NRC since 2006 have totaled $444 million. Since nuclear power generation is justifiably a heavily regulated industry, that is not a shocking figure. However, these plants are also regulated by several other agencies. The two largest NRC rules cover “Fitness for Duty” and post 9/11 security standards. The Fitness for Duty measure costs $481 million and is aimed at combating worker fatigue and improving drug and alcohol testing at facilities. The second largest rule, perhaps not surprisingly, covered 9/11 security requirements. The 2009 regulation estimated that an average nuclear site incurred $1.7 million in initial costs, with roughly $600,000 in annual recurring burdens. The total costs of the rule were $154 million, with $38 million in annual costs for the entire industry.

In addition, other agencies have issued power plant regulations that directly affect the nuclear industry. For example, the Environmental Protection Agency (EPA) has issued a rule for cooling water intake structures, at $7.3 billion in total costs on the energy production sector, in addition to a major rule covering “Effluent Limitations Guidelines and Standards” ($471 million in costs). The measures will affect virtually every power plant near a body of water including nuclear facilities.

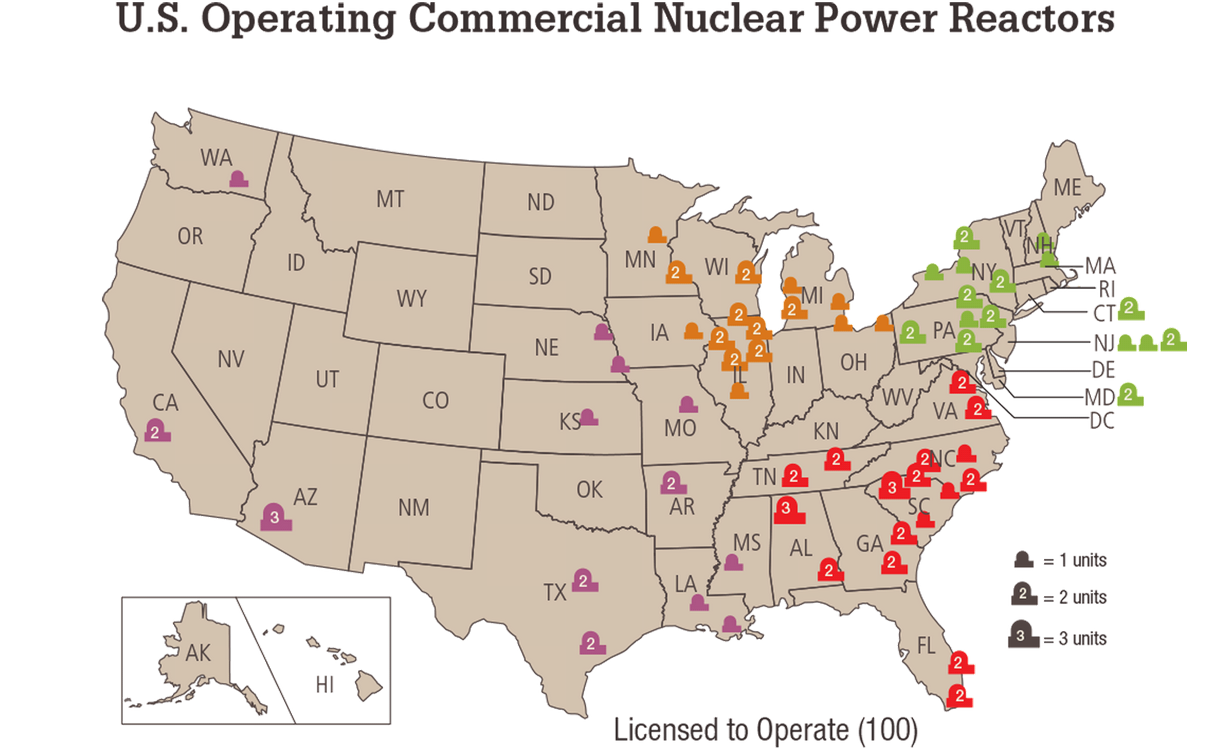
According to the Energy Information Administration (EIA), there are only 61 nuclear power plants in the nation that house 100 total reactors, displayed on the following map.

Currently, NRC displays a paperwork cost of $2.2 million from its 10.5 million paperwork hours. However, this that only amounts to about 20 cents an hour for those performing the paperwork. As AAF has previously found, a thorough examination of NRC’s paperwork slate uncovers more than $257 million in unpublished costs, or 116 times the reported figure. This results in a per-facility recordkeeping cost of $4.2 million.

Simply dividing the hours by the number of nuclear power plants yields an astounding 173,459 hours per facility. Assuming 2,000 hours a year per employee, that’s the equivalent of 86 full-time equivalent (FTE) employees per plant. Naturally, every facility likely does not employ 86 workers to focus exclusively on regulatory compliance. Given the federal government’s total imposition (10.5 billion hours), 10.5 million hours might seem pedestrian. The overall numbers aren’t large, but given the number of affected facilities, the relative burden on nuclear power plants is notable. For comparison, of the roughly 1,544 power plants in the U.S., only about four percent are nuclear-powered, yet they produce around 20 percent of the nation’s electricity.

What are the main drivers of nuclear plant regulation, at least in terms of paperwork? According to the Office of Information and Regulatory Affairs (OIRA), a prime culprit is written guidance to the states on ensuring that, “the radiation control program … remains adequate and compatible with [existing federal law].” From just 58 state and local respondents, this seemingly pedestrian requirement will generate 285,143 hours on local governments. Strangely, the listed costs are $0, but the supporting statement notes the burdens exceed $78 million or more than $1 million locality.

Another notable requirement surrounds “Reactor Site Criteria,” which “establishes approval requirements for proposed sites for the purpose of constructing and operating stationary power.” At 167,000 hours from just two respondents, the 83,000-hour burden per entity essentially represents the years of planning and development that first must take place before NRC and other regulators license a site to produce power. For example, NRC and OIRA estimate “non-seismic siting criteria” will take 22,000 hours (roughly 11 FTEs) and “geologic and seismic siting criteria” will consume 51,000 hours of time (25 FTEs). This assumes 2.3 applications annually, yielding 167,000 hours and more than $45 million in costs.

In other words, just an approval for the site of a reactor can cost close to $20 million per entity. This is not to say $20 million isn’t an appropriate price to establish safety standards for a new plant. Given the lengthy review times by NRC however, $20 million can be a fraction of the total investment required to get approval for a new power plant.

During the last five years, NRC has taken twice the amount of time to review license renewal and uprate applications (increasing the output of  a plant). Likewise, “Early Site Permits” now take about six years, up from an already prohibitive three to four years. Combined licenses now take about eight years for NRC to process, up from four a few years ago. These delays obviously cost money and heighten uncertainty in an industry trying to compete with other energy sources.

Finally, the third most burdensome collection according to OIRA, involves a request for information after the Fukushima nuclear disaster in Japan. The survey, requesting data on seismic and flooding hazards, was intended to determine if more regulation would be needed in the future. Once again, the listed costs are $0, but the supplemental data reveals annualized costs of $29 million and $87 million in total costs on the industry. For example, the seismic risk reassessment will cost $55 million and an assessment of flooding hazards will impose $14.7 million in burdens. This routine collection of information, imposed on one industry, nevertheless has significant effects on each site.

Paperwork is just one aspect of the regulatory costs the nuclear industry must navigate annually. Unlike other power generation sources, there is a premium placed on security and this premium comes at a price. Some estimates place the number of security personnel at nuclear sites at 9,000 for just 61 plants. That incredible figure equals roughly 140 guards per facility. Generally, power plants must be able to deter “a well-trained and dedicated paramilitary force, armed with automatic weapons and explosives and intent on forcing its way into the plant to commit radiological sabotage.” This is an important, but expensive, safety apparatus all plants must maintain.

According to the Bureau of Labor Statistics (BLS), there are 5,190 security workers directly employed by the nuclear industry, with the balance of the 9,000 estimate likely consisting of contract staff. For the 5,190 employees, 640 are supervisors, with an annual wage of $69,360; the remaining staff earn $50,070 a year. In compensation costs alone, the nuclear industry pays $272.2 million for security or $4.4 million per facility. This figure excludes non-wage benefits and other overhead associated with staffing roughly 9,000 security personnel. In addition to the paperwork burden ($4.2 million plus $4.4 million), there are at least $8.6 million in costs per plant, exclusive of fees, employee benefits, overhead, capital, and other regulatory burdens.

Benefits

Beyond the costs of nuclear regulation, from the security staff to the capital and paperwork burdens, there are generally legitimate reasons for these federal rules, such as the value of having nuclear power plants safe from the threat of major earthquakes, flooding, or terrorist attacks. Generally, federal agencies have difficulty monetizing or even quantifying these benefits. As an independent agency, NRC rarely conducts comprehensive benefit-cost analysis.

However, agencies sometimes use a “break-even analysis” when benefits are difficult to monetize. In other words, a break-even analysis asks, “What would the benefits need to be to justify the costs.” There are two exemplars for examining the benefits of nuclear regulation: the Three-Mile Island accident and the destruction of the Fukushima power plant.

For example, estimates of the total economic loss from the Fukushima disaster are upwards of $500 billion, from abandoned cities and towns more than 310 square-miles around the reactor to the 159,000 people displaced from their homes. In addition, 56 percent of all the fish caught off of the coast of Japan were contaminated. For the Three-Mile Island incident, there are estimates that the clean-up alone cost nearly $1 billion, although there were no direct fatalities from the accident. Finally, there are the occupational safety benefits. Generally, the nuclear industry has one of the highest safety records in the nation. There are roughly just 0.03 accidents per 200,000 workers, based on the latest data.

No one regulation can eliminate the risk of a $500 billion meltdown or avoid $1 billion in clean-up costs. Yet regulators often point to the ability to lower the possible risk of these accidents occurring or how rule after rule can cumulatively contribute to a safer workplace and secure facilities. The costs of nuclear regulation are certainly significant, but regulators will note the benefits of an avoided disaster are likely much higher.

The Fees

In addition to the direct and indirect regulatory costs are the fees operators pay to the NRC. Coal and natural gas facilities do not fund EPA’s budget; taxpayers do. However, nuclear power plants are responsible for roughly $885 million in annual fees to the NRC and others, or about $14 million per facility. The remaining ten percent of NRC’s budget is provided by the U.S. Treasury. Combined with regulatory costs, the total cost per facility eclipses $22 million.

There is some debate on the amount of “overhead” at NRC compared to other agencies. For example, its peer agencies spend about 20 to 32 percent on overhead costs, compared to 37 percent at NRC. Congress responded to this inequity and the FY 2016 budget limited overhead to 34 percent. This was effective, but the FY 2017 Budget once again requested increased overhead, making it one of the leading agencies to spend money outside of its statutory objective.

Clean Power Plan

For the future of the nuclear industry, there are few regulations as important as the Clean Power Plan (CPP). It does encourage states to switch to low carbon energy sources, but the industry is hardly more competitive because of the CPP. As former Secretary of Energy under President Obama, Steven Chu, noted, “Even though the Clean Power Plan says we need nuclear and maintains the same ratio, they give no credit for it.”

Essentially, the CPP allows credits for new nuclear facilities or expensive uprates at existing facilities, but there are no additional credits to the current fleet. However, plants under construction do count toward compliance once they are in operation. The industry pointed out the retiring nuclear plants will likely be replaced by newer efficient natural gas plants, increasing greenhouse gas emissions. There are roughly 10-15 plants in danger of shutting down during the next five to ten years, according to Marvin Fertel of the Nuclear Energy Institute. He noted, “If we were to lose all those plants, and assuming they were replaced with the most high-efficiency combined cycle gas plants, it would wipe out approximately one-quarter of the gains achieved by the Clean Power Plan [CPP], if it was implemented.” Given the costs of relicensing and the treatment under the CPP, it is likely the current fleet could continue to experience retirements.

Reforms

The NRC must take some steps to expedite the process of application approval. Beyond the sheer capital and paperwork costs associated with nuclear regulation, time equals money. In some instances, it can take eight years to review and approve licenses. For all the talk about delays in promulgating new regulation, delayed regulatory approvals are equally as troubling. During the last decade, fees have increased, as have review times. For other agencies, notably the Federal Communications Commission, Congress has mentioned the idea of “shot clocks” for regulatory approval. There are plenty of incentives for Congress, policymakers, and NRC to work together on flexible timelines for application review. Trimming review times and some regulatory costs could help to achieve greater cost competitiveness for the nuclear industry.

As mentioned above, NRC spends a considerably higher portion of its budget on overhead than other peer independent agencies. Despite some attempts from Congress to control these costs, NRC once again requested higher funding, overall and for overhead specifically. In the future, Congress could consider a permanent cap on NRC’s overhead budget. This need not be a firm and fixed amount initially; it could be phased in gradually to ensure taxpayers aren’t paying for the agency’s extraneous overhead costs.

Conclusion

Regulation for the nuclear industry is inherently unique and it should never be deregulated in the same manner as other industries. However, there are incremental and meaningful steps policymakers and regulators can take to alleviate a regulatory burden of at least $8.6 million per plant, exclusive of fees and other major capital costs. Ensuring a balanced regulatory approach that can expedite licenses and continue to protect the safety of nuclear facilities is critical to the future of the industry and low-carbon energy options.